Pattern making connects fundamental physics and geometry. This article explores the mathematical principles underlying pattern construction, focusing on dart symmetry and the Gauss-Bonnet theorem.
Dart Symmetry and Noether's Theorem
The first fundamental principle in garment design is the dart symmetry principle: the rotational symmetry of a dart around its apex.
In practice, you can move a dart anywhere along the outline of a pattern without changing the fit of the garment, as long as it still points toward the same point.
This connects to fundamental physics through Noether's Theorem, which states that every continuous symmetry corresponds to a conserved quantity:
- Time symmetry → conservation of energy
- Space symmetry → conservation of momentum
- Dart rotation → conservation of curvature
Mathematically, this conservation comes from geometry: all the curvature is concentrated at the dart apex. Moving the dart doesn't change the total curvature, it just redistributes it.
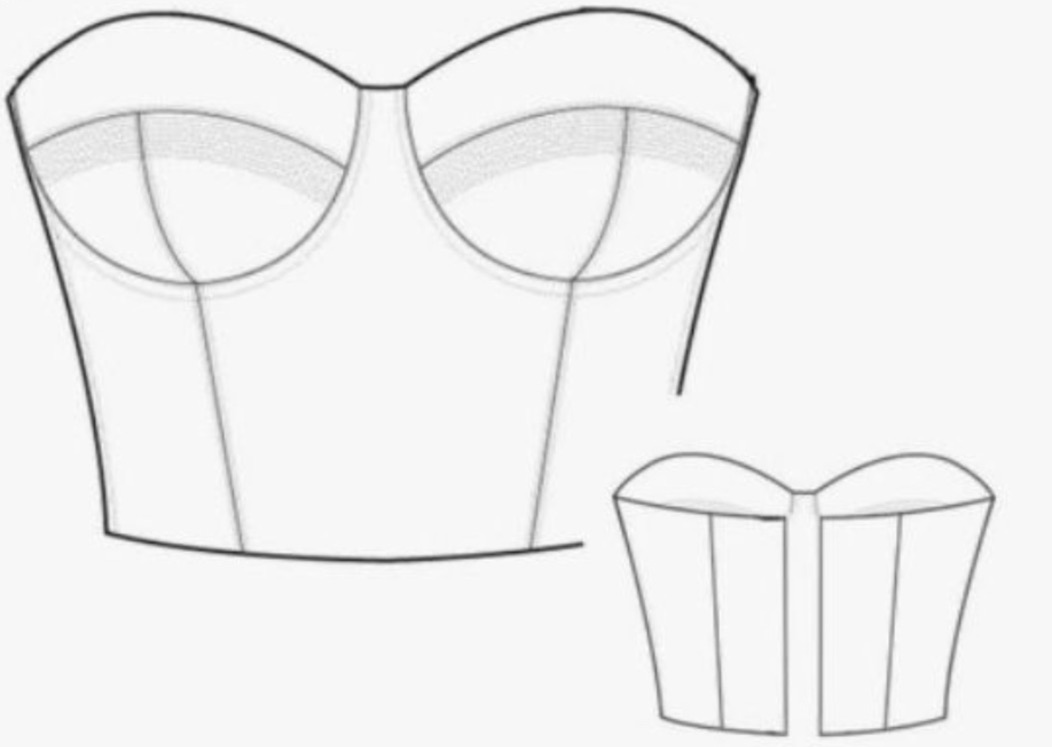
Credit: Photo taken from Helen Armstrong's book, Pattern Making for Fashion Design.
Originally shared on LinkedIn
The Gauss-Bonnet Theorem
Surface geometry and pattern geometry are fundamentally connected through the Gauss-Bonnet Theorem, which connects a surface's curvature to its topology.
The Geometric Role of the Dart
In a stitched garment, the fabric follows the non-flat, curved shape of the body. Curvature is concentrated at points like the bust. The pattern must account for this curvature through precise geometric relationships, ensuring the total curvature is properly distributed.
The dart acts as the geometric mechanism that handles this transformation. The sum of the angles along the dart perimeter must exactly compensate for the curvature that was concentrated in the stitched garment.
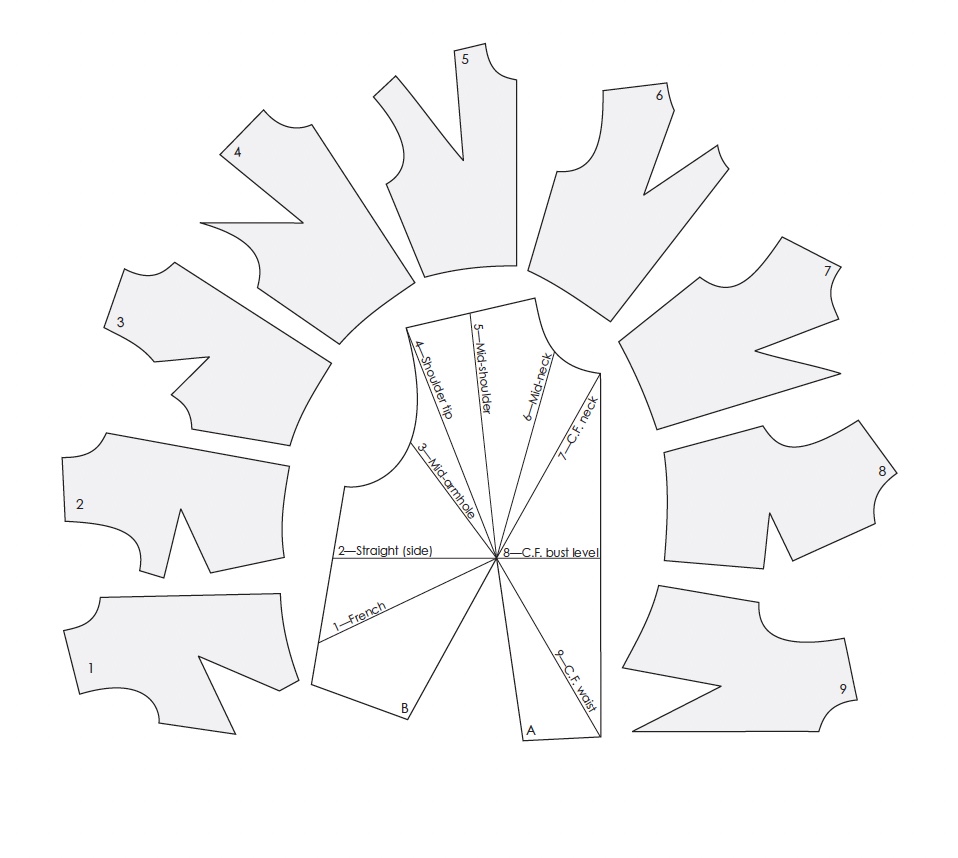
Angles in Pattern Geometry
Most pattern-making books teach the "recipe," but the underlying equation reveals why it works. Angles are fundamental to the geometry of fit: they aren't secondary details, but first-class citizens in pattern construction.

Calculating dart angles with Gauss-Bonnet theorem. Calculation taken from a presentation I gave at Zalando.
Originally shared on LinkedIn